
▲오른쪽부터 예종철 교수, 한요섭 연구원, 차은주 연구원
[이미지 제공=KAIST, 저작권자로부터 이미지 사용 허락을 받음]
이달 10일 카이스트 대학 바이오 및 뇌공학과 예종철 석좌교수 연구팀이 4차 산업혁명의 핵심기술인 인공지능의 딥러닝의 구현 방법인 심층 신경망의 수학적 원리를 밝혀냈다.
심층 신경망은 인공지능의 핵심을 구성하는 딥러닝의 대표적인 구현 방법이다. 이것을 이용한 분야는 이미 사람의 기술을 훨씬 뛰어넘고 있다. 하지만 이런 뛰어난 성능을 가진 심층 신경망은 아직 제대로 된 작동 방법이 정확히 규정되어 있지 않아 여러 문제들이 발생한다.
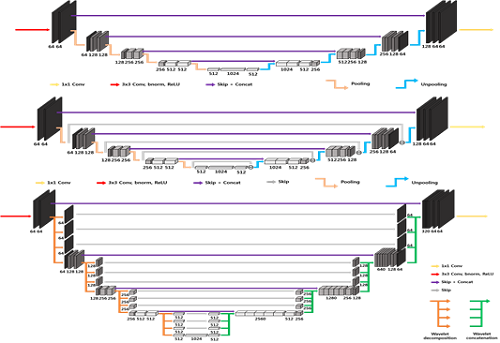
▲수학적인 원리를 이용한 심층 신경망의 설계 예시
[이미지 제공=KAIST, 저작권자로부터 이미지 사용 허락을 받음]
그 때문에 연구팀은 심층 신경망의 구조가 얻어지는 고차원적인 공간 속에서 기하학적인 구조를 찾기 위해 노력했다. 그 결과로 기존에 신호처리 분야에서 집중적으로 연구된 고차원 구조(행켈구조 행렬)를 기저 함수로 분해하는 과정에서 심층 신경망 구조가 나오는 것을 발견했다. 그리고 행켈 행렬이 기저 함수로 나뉘는 과정에서 나눠진 광역 기저 함수와 국지 기저 함수가 각각 인공지능의 풀링과 필터링 역할을 한다는 것을 밝혔다.
이 연구팀의 ‘심층 합성곱 프레임렛(Deep Convolutional Framelets)’이라는 새로운 조화 분석학적 기술은 인공지능의 블랙박스 역할을 하는 심층 신경망의 수학적 원리를 밝혔다.

[이미지 제공=KAIST, 저작권자로부터 이미지 사용 허락을 받음]
연구팀은 이 결과를 영상 화소 복원, 영상 잡음 제거, 의료 영상 복원 문제에 적용을 해보았고 그 결과 영상에서 80%가 화소가 사라진 사진을 복원하는 기능과 사라진 영상의 자세한 디테일을 복원하는 기능이 기존 인공신경망보다 훨씬 우수한 것으로 확인되었다.
우리는 이번 연구를 통해서 기존의 심층 신경망과는 달리 원하는 응용분야에 따라 최적화된 구조를 수학적으로 디자인하고 이전과는 다르게 그 결과를 예측할 수 있게 되었다. 또한 이러한 결과를 통해 설명 가능한 인공지능이 필요한 모든 분야에 적용이 가능하게 되었다.
이번 연구는 예종철 석좌교수와 한요섭 연구원, 차은주 연구원이 진행하였고 그 결과는 응용 수학 분야 국제 학술지인 'SIAM Journal on Imaging Sciences'에 4월 26일 자 온라인판에도 게재됐다.
[대한민국청소년기자단 IT·과학부=7기 성소현 기자]







 암컷만 태어나는 초파리 미스터리, 비밀은 '세균'?
암컷만 태어나는 초파리 미스터리, 비밀은 '세균'?
 제주 4.3사건 70주년을 맞아 방문한 제주 4.3 평화공원
제주 4.3사건 70주년을 맞아 방문한 제주 4.3 평화공원


