우리가 지금 몇 차원 세계에서 살고 계신지 알고 계신가요? 물론 모르시는 분들도 계실 수 있으시겠지만, 대부분의 사람들은 알고 있을 것 같다. 맞습니다. 바로 3차원이다. 제가 오늘 설명해드리고 싶은 주제는 차원에 대해서이다.
우선, 차원이란? Dimension으로, 수학에서 공간 안에 있는 점과 선 등의 위치를 나타내는 위해서 필요한 축의 개수를 말한다. 이로 인해, 차원은 0차원에서 시작하여 1차원, 2차원, 3차원, 4차원에서 n차원까지 나타낼 수 있다.
0차원은 쉽게 말해서 점이라고 할 수 있다. 하나의 공간 즉, 차원 안에서 단 하나의 점밖에 없는 공간이다. 우리가 수학 시간에 배운 x축과 y축 그 무엇도 없는 (0,0) 원점의 공간이라고 생각할 수 있다.
1차원은 쉽게 말해서 직선과 곡선이라고 할 수 있다. x좌표만 존재하여서 x좌표에서의 선상에서의 이동만 가능한 공간이라고 할 수 있다. 수직선을 생각해보면 이해하시기에 쉬울 것 같다. 끝이 없이 이어진 수직선과 같이 –10부터 0을 지나 10까지 이어지는 한 직선의 공간을 1차원이라고 한다.
2차원은 쉽게 말해서 면이라고 할 수 있다. 1차원과 달리 x좌표와 y좌표가 존재하여서 x좌표에서만 이동할 수 있었던 선과 달리 y좌표에서도 이동이 가능하여서 (1,5)처럼 직사각형 도형이 평면에 생길 수 있다. 이 뿐만 아니라 다양한 평면도형이 존재할 수 있다. 앞서 말씀드렸던 직사각형뿐만 아니라 삼각형, 정사각형, 오각형 등 다양한 도형이 존재할 수 있다. 또한 1차원에서는 곡선으로만 존재하였지만, 2차원에서는 곡선으로 이용된 도형인 원도 존재한다.
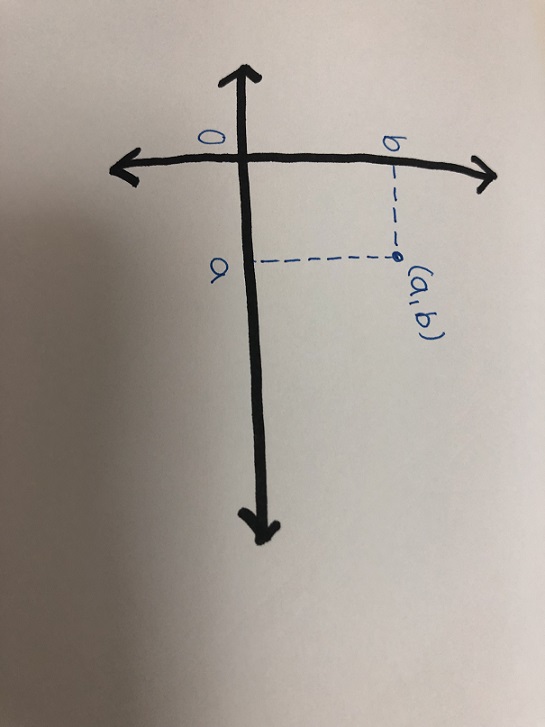
[이미지 촬영=대한민국청소년기자단 11기 이윤서기자]
3차원은 쉽게 말해서 입체도형 즉, 입체라고 할 수 있다. 2차원의 세계보다는 조금 더 발전한 것이라고 할 수 있으며, 현재 우리가 살아가고 있는 차원의 세계이다. 기존에 있었던 x좌표, y좌표 뿐만 아니라 z좌표가 생겨나면서 입체가 생겨날 수 있게 된 것이다. z좌표는 간단하게 말해 세로축 높이라고 할 수 있다. y좌표는 누운 세로라고 한다면, z좌표는 위로 뻗은, 높이를 나타낼 수 있게 해주는 또 다른 세로축이라고 말 할 수 있다. 밑 사진과 같이 z좌표는 x축, y축과 직각을 이루고 있다. 또한, 이 세 좌표들을 이용해 구와 정육각형 등 다양한 입체도형을 만들 수 있다.
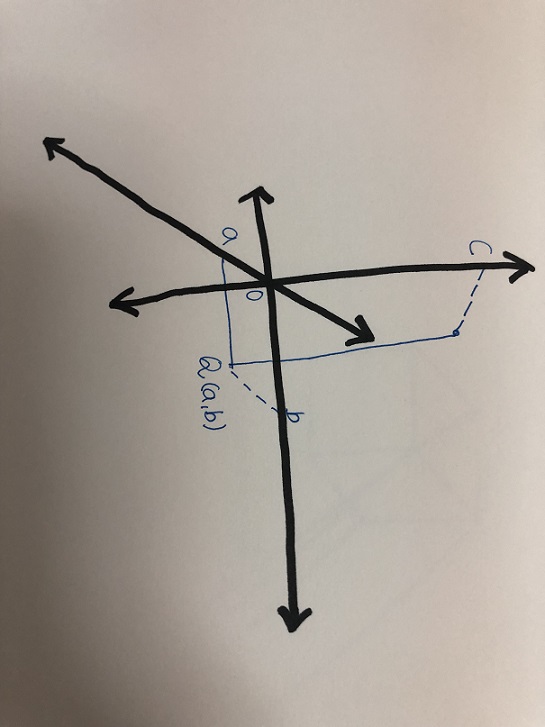
[이미지 촬영=대한민국청소년기자단 11기 이윤서기자]
4차원은 쉽게 말해서 공간 안에서의 시간 이동이라고 할 수 있다. 3차원에서 있었던 x좌표, y좌표, z좌표 뿐만 아니라 t좌표가 생기면 시간 이동을 할 수 있게 된다. 우리가 실제로 경험하는 차원의 세계가 아니기 때문에 무엇이 변화되는지 모든 것을 알 수 없다. 하지만 4차원의 세계를 요즘 SF영화 등에서 표현되고 있기 때문에 이러한 장르를 좋아하시는 분들이시라면 4차원의 세계도 접해볼 수 있을 것 같다. 3차원의 세계는 선 3개를 사용하여서 입체도형을 만들었지만, 4차원의 세계는 시간과 공간이 만나기 때문에 선 4개가 수직으로 만나는 도형이 생겨날 것이다. 우리가 살아가면서 시간이 흘러가고 있기 때문에 4차원의 세계라고 주장은 할 수 있다. 하지만, 시간은 우리가 다룰 수 없기 때문에 우리는 아직 3차원의 세계 속에서 살아가고 있다.
4차원과 마찬가지로 5차원 역시 우리가 살아가는 차원의 세계가 아니기 때문에 가설들만 있다. 가설들 중 대표적인 것은 블랙홀과 생명이다. 블랙홀은 4차원의 세계를 조금 더 확실하게 알려줄 수 있는 유일한 것이라고 하여 4차원의 세계 다음에 존재할 5차원의 세계라고 몇몇 사람들이 말하고 있다. 블랙홀뿐만 아니라 생명도 5차원의 가설에 포함된다. 4차원까지는 시간과 공간이라고 주장하였지만, 5차원에서는 시간과 공간, 생명까지 존재한다고 가설하고 있다. 즉, 우리가 존재하고 있는 공간뿐만 아니라 다른 시간 축에 따라 무수하게 공간에 존재하고 있는 것이다. 다른 시간 축의 공간에서도 내가 존재할 수 있고, 자신과 완전히 같은 운명을 맞이하고 있을 수도 있고, 반대되는 운명에 도달하고 있을 수 있는 것을 5차원 세계의 가설이라고 볼 수 있다.
[대한민국청소년기자단 IT·과학부=11기 이윤서기자]







 색다른 서울 근현대사 탐방하기
색다른 서울 근현대사 탐방하기
 누구나 알기에, 의미를 잘 분별해서 들어야 할 동요, '우리 집에 ...
누구나 알기에, 의미를 잘 분별해서 들어야 할 동요, '우리 집에 ...


